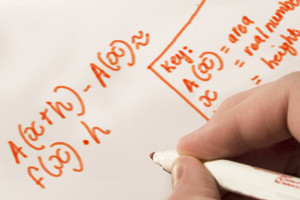
Fundamental Theorem of Integral Calculus
Fundamental Theorem of Integral Calculus
What You Will Learn In This Free Course
- -
- -
- -
- -
Complete This CPD Accredited Course & Get Your Certificate!
Certify Your Skills
A CPD accredited Alison Diploma/Certificate certifies the skills you’ve learnedStand Out From The Crowd
Add your Alison Certification to your resumé and stay ahead of the competitionAdvance in Your Career
Share your Alison Certification with potential employers to show off your skills and capabilities
Learner Reviews & Feedback
Fundamental Theorem of Integral Calculus
Want to create a customised learning path for your team?
Our dedicated Learning Advisors are here to help you curate a customised learning path tailored to your organisation's needs and goals.
Not sure where to begin?
Discover the career most suitable for you and get started in the field with a step-by-step plan.
Get your Plan










 Avg. Hours
Avg. Hours  Contains Video
Contains Video  CPD Accredited
CPD Accredited 
 Total XP:
Total XP: 
 Knowledge & Skills You Will Learn
Knowledge & Skills You Will Learn 







