This course on the applications and properties of definite integrals introduces you to estimating with Riemann sums, sigma notation, properties of a definite integral and the fundamental theorems of integral calculus. You will learn about the trapezoid approximation methods used in evaluating integrals, and about sigma notation, which is a convenient way to compress writing large sums during integration. An exciting part of sigma notation is that it can be used for sums involving subscripts and you will study the three important laws that govern it. See how to get the exact area under a curve by using an approximation and subintervals and then taking the limit as a function approaches infinity.
The course continues by describing the properties of definite integrals. Do you know that the average set of numbers lies between the smallest and largest number but doesn't have to be a set member? The definite integral enables us to take the average of infinitely many numbers! The material describes the essence of the mean value theorem for integrals. You will delve into the relationship between a definite integral and the area under a curve. Have you experienced instances in the application of integration where the definite integral does not always yield an area under a curve? This is because of the basic rules of anti-differentiation. Unfortunately, most expressions occur in a format that doesn't allow for an immediate reversal of the process of differentiation or integration, therefore, additional methods must be developed. You will be introduced to different methods and techniques used in integration to solve problems and learn how to use a substitution equation for conversions.
Furthermore, knowing how to differentiate basic trigonometric functions makes the process of finding many integrals easier. Learn about the concept of combined sine and cosine functions as well as trigonometric integrals using u-substitutions. You will also be taken through combined tangent and secant functions. Did you know that trigonometric substitutions can be useful in integrating certain binomials? You will discuss the natural logarithmic functions and integration by partial fractions. In order to use this method, we must first decompose a fractional integrand into the sum of simpler fractions. At the end, you will be taken through a slightly more complicated type of first-order differential equation. If you are a student looking to improve your knowledge of integral calculus and its amazing applications, then register for this course today. It is free to anyone, including those revising for the Advanced Placement (AP) calculus exams.
What You Will Learn In This Free Course
View All Learning Outcomes View Less All Alison courses are free to enrol, study, and complete. To successfully complete this Certificate course and become an Alison Graduate, you need to achieve 80% or higher in each course assessment.
Once you have completed this Certificate course, you have the option to acquire an official Certificate, which is a great way to share your achievement with the world.
Your Alison certificate is:
- Ideal for sharing with potential employers.
- Great for your CV, professional social media profiles, and job applications.
- An indication of your commitment to continuously learn, upskill, and achieve high results.
- An incentive for you to continue empowering yourself through lifelong learning.
Alison offers 2 types of Certificate for completed Certificate courses:
- Digital Certificate: a downloadable Certificate in PDF format immediately available to you when you complete your purchase.
- Physical Certificate: a physical version of your officially branded and security-marked Certificate
All Certificate are available to purchase through the Alison Shop. For more information on purchasing Alison Certificate, please visit our FAQs. If you decide not to purchase your Alison Certificate, you can still demonstrate your achievement by sharing your Learner Record or Learner Achievement Verification, both of which are accessible from your Account Settings.
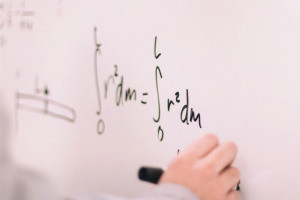










 Avg. Hours
Avg. Hours  Contains Video
Contains Video  CPD Accredited
CPD Accredited 
 Total XP:
Total XP: 
 Knowledge & Skills You Will Learn
Knowledge & Skills You Will Learn 







